To me, mathematics is an ivory tower.
An ivory tower, vast, complex, and beautiful.
With its doors wide open.
At each level, helping hands are offered,
Trying to help you up the stairs.
However, the steps are steep
And there is no elevator.
No-one can carry you up.
You need to take the steps by yourself.
If you climb just a little
And open your eyes,
The view will be spectacular.
What’s on Your Napkin?
Either nature or my brain or both do a wonderful job of clustering related things for me so that I often feel coming along many related things within a short time. Recently, I read Stuart L. Pimm‘s wonderful The World According to Pimm: a Scientist Audits the Earth. It contains the following sentence:
« Robert Colwell, an ecologist from the University of Connecticut, and I were sitting in a bar drinking Antarctica and excitedly drawing lines on paper napkins, the preferred medium of serious scientific discourse worldwide. »
Shortly afterwards, I learned about the blog What’s on my blackboard? showing people’s blackboards (or whiteboards) which are often stunning.
Hence my question: what’s on your napkin? I dare you: grab your smartphones and share images of your napkins full of scientific sketches and/or formulas!
Regular Viruses
As long as they do not infect us, viruses are nothing but fascinating. One aspect of this fascination is based on the shapes of viruses. Looking at electron microscopy images of viruses or at computer models based on X-ray crystallography, my impression is that mother nature has copied from a geometry book. This impression is echoed by what you find in books and papers on virology. Why do biologists think about possible polyhedra with icosahedral symmetry? Why is it that many viruses have the shape of such polyhedra? For some years, it seemed like biologists had a very accurate theory of the construction of such regular viruses. Advances in imaging have left them less confident but with an even higher appreciation of the formation of biological shapes.
Neighbourly Polyhedra
In the plane, it is relatively easy to find four convex polygons which pairwise share an edge and are otherwise disjoint. Can you find five polygons in the plane with these properties? How about polyhedra? How many polyhedra can you find such that any pair of them share a face and are otherwise disjoint?
For me, this is an example where my three-dimensional imagination fails utterly. If you have never thought about this before, I suggest to try finding as many such polyhedra as possible (why not start with seven?) before reading on.
Dating
Whatever your primary association to the heading of this post may be, the main characters in this story are elephants’ teeth and stars. Inspired by Jon Kalb’s book Adventures in the Bone Trade, I will discuss two aspects of the question: how old is this place or thing?
Beauty in Patents
In an earlier post, I wondered about the hidden beauty of scientific illustrations in books which are read only by very few specialists. A similar situation is found in the context of patents. They usually come with clarifying sketches or illustrations which range from sloppy to artistic.
Not later than from the moment Richard Buckminster Fuller filed his patent on cartography in 1944, mathematical beauty had found its way into patent applications. How many hidden gems may there be in patents? At least, having patents available online makes it a lot easier to spot some.
Soap Bubbles: a Paradise for Kids and Math Nerds
Soap bubbles are simply irresistible. As is the heading of Section 4.3 of Roberto Piazza‘s book Soft Matter, so I had to borrow it for this post. In the book, you can learn about some of the wonderful physical properties of soap bubbles. For example, I was not aware that each bubble is a double shell enclosing water in between. In this way, the hydrophilic heads of the soap molecules point inside whereas the hydrophobic tails point outside. The colours are then created by interference of light reflected from the two soap films. As water flows and evaporates between the films, colours change depending on the distance between the two films.
Perspectiva Corporum Regularium
Most of the time, I enjoy how one book leads to another in a seemingly endless bibliophilic journey into the past (it is a pity that books usually cannot refer to future books). This time it is the book Shaping Space (see short review) referring to a book with very few words and many wonderful drawings of polyhedra: Wenzel Jamnitzer’s Perspectiva Corporum Regularium from 1568.
Zeolites
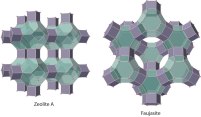
One of the books I am currently reading is Roberto Piazza‘s Soft Matter (see here and here for reviews) . In the book, there is a short paragraph on zeolites which left me wishing for more information. In particular, there was no illustration of a zeolite. A quick image search convinced me that this topic is a perfect fit for my blog.
So what is a zeolite? Zeolites form a class of minerals composed of aluminium, silicon, and oxygen. They form a very regular arrangement of pores which makes them highly useful in industrial applications.
The Groups of the Tetrahedron, the Octahedron, and the Icosahedron
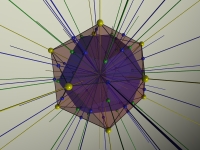After discussing the dihedral group, it is time to post my images of how Klein introduces the symmetry groups of the tetrahedron, the octahedron and the icosahedron.
By duality, this also handles the case of the dodecahedron (it is the dual of the icosahedron) and that of the cube (it is the dual of the octahedron) and thus all the Platonic solids are covered.
Glimpses of a fascinating world 
